Backpropagation in Machine Learning – Complete Guide

In this Article. we will explore Backpropagation in Machine Learning and how it works on data to perform predictive modeling.

If you’re familiar with machine learning, you’ve probably heard the term backpropagation before, even if you don’t know what it means.

But how does backpropagation work? This article explains backpropagation in the context of machine learning.

How it works in a neural network to teach the network, and why this algorithm is so effective at training neural networks and other machine learning models.

Backpropagation or backprop as it’s commonly abbreviated is an algorithm used in artificial neural networks to calculate the gradient of an output error with respect to an input vector, used in training neural networks by supervised machine learning algorithms such as gradient descent and the generalized delta rule.

This helps determine how much each input should be adjusted to reduce or increase the network’s output error.

Backpropagation has been widely used in recent years in fields such as computer vision, natural language processing, speech recognition, and robotics. Here’s what you need to know about backpropagation in machine learning.

What Is Backpropagation In machine learning?

In machine learning, backpropagation is a widely utilized algorithm or technique to train a model with trial and error use in training feedforward neural networks.

Generalizations of backpropagation live for different artificial neural networks (ANNs) and for other machine learning algorithms for functions generally.

Imagine you have a neural network for digit recognition: an input layer for pixels, three hidden layers with sigmoid activation functions, and one output layer that gives us a probability between 0 and 1 of which digit was recognized.

To train such a model, you would use a loss function (like cross-entropy) to compare predicted outputs and real outputs with backpropagation, these errors are then fed forward through the network so that weights can be adjusted accordingly.

This iterative approach allows networks like these to learn more complex representations than they could if only trained from inputs.

Where Backpropagation Comes from?

A simple form of backpropagation was published by Seppo Linnainmaa in 1970, but it only propagated one error derivative at each layer.

Rumelhart and Hinton proposed an extended form that propagates multiple error derivatives.

A commonly-used implementation is due to Williams, Popular implementations include vanilla BFGS, SGD, and RMSprop.

The computational complexity ranges from cubic to quadratic in the number of neurons per layer.

Related Article: Autoencoders: Introduction to Neural Networks

How Does Backpropagation Work in Machine Learning ?

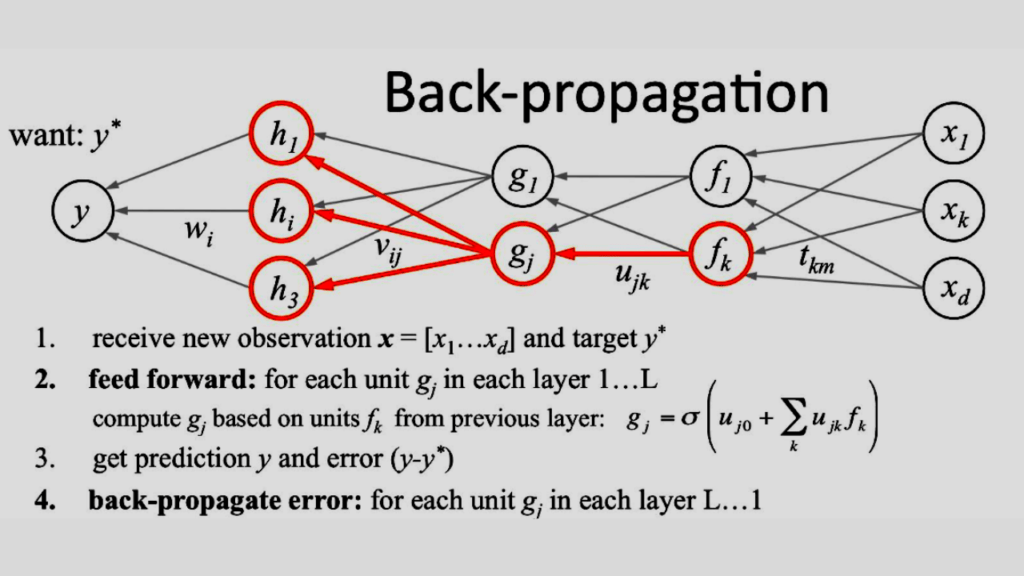
In order to understand how backpropagation works, it’s helpful to see how feedforward neural networks work.

These are some of our most basic artificial neural networks, and they’re quite easy to understand.

You can think of these as graphs with input nodes, hidden layers (where computation happens), and output nodes.

Here’s a simple example There is an input layer that takes in numbers; then there is a single layer for computing something.

Finally, there is an output layer that gives us a number we want. So you can think of an ANN like a function:

ƒ(x) = s(w x + b)

It takes in parameters w and b, applies its weights and biases, does some computations using those parameters, outputs s(w x + b) where s is your activation function that determines whether your final value is 1 or 0.

How Can I Implement backpropagation in machine learning?

Implementing backpropagation is not a difficult task, although you will need some understanding of how neural networks work.

If you are unfamiliar with backpropagation and neural networks, then explore more about backpropagation in machine learning as well as ANN.

Basic knowledge of calculus will be useful as well, To implement backpropagation, you will typically write code for one or more neurons in your network,

Each neuron takes input from other neurons and produces an output value that is passed along to other neurons as input values.

Each input value (x) can take on multiple values (xi), but only one value at a time passes into each neuron; once a neuron has calculated its output value (y), it passes its output on to all neurons that receive inputs from it, including itself.

Why We Need backpropagation in machine learning?

The primary benefit of Backpropagation in a deep learning network, it has the ability to learn multiple levels of abstraction without manual intervention.

It learns higher-level features through interactions with lower-level features rather than being explicitly programmed at each level.

This property can be exploited by performing gradient descent on error derivatives until convergence with respect to certain parameters is achieved.

Error derivatives can be computed using automatic differentiation (AD), While AD provides an elegant solution to many issues that arise during numerical computation.

It also brings along new challenges such as maintaining consistent gradients during backpropagation that typically do not exist in hand-coded implementations of gradient descent.

Different Types of Backpropagation Networks

1. ANN:

ANNs and MLPs are mostly suited for classification & regression problems, whereas CNNs, RNNs & GPs excel at pattern recognition & time series modeling applications

2. Fully-Connected Feedforward Networks:

This is where all nodes are fully connected to all other nodes with the different neural network layers.

Related Article: Feed Forward Neural Networks Ultimate Guide Explained

3. Convolutional Neural Networks (CNNs):

An extremely powerful type of neural network that has achieved huge success on certain visual recognition tasks such as ImageNet.

4. Recurrent Neural Networks (RNNs):

These types of networks have become extremely popular due to their ability to capture temporal patterns found in sequence data such as text, speech, and time series.

RNNs are typically not used for classification or regression, but instead for problems like machine translation, sentiment analysis, and anomaly detection.

5. Graphical Models:

Probabilistic graphical models represent conditional independencies between random variables.

Different layers can then be trained using backpropagation with a variant known as conjugate gradient descent.

Key Points in Backpropagation

The general algorithm for backpropagation involves 3 steps: A.

1. Forward Propagation:

During forward propagation, we calculate each of our network’s outputs (i.e., activations) based on its inputs. B.

2. Error Calculation:

Once we have all of our network’s outputs, we can then proceed to compute each error value the difference between a neuron’s desired output and its actual output. C.

3. Weight Adjustment/Backward Propagation:

After we’ve calculated all of our errors, we can then adjust all of our weights in an attempt to reduce them (and thus improve accuracy).

Note: In practice, there are several additional details you will need to consider if you want your implementation to be accurate.

These include making sure that your calculation is able to prevent overflow during summation as well as dealing with dead neurons or neurons that go off the scale.

Matrix Multiplication in Backpropagation

The key idea of backpropagation is very simple and can be illustrated using just one hidden layer.

x’ = Wx + b

Suppose we have a neural network with one input unit, one output unit, and three hidden units: A single hidden layer is sufficient for many practical problems.

In particular, suppose our task is to compute (x’, y’) = Ax + By for some known vector x and vector y.

Each element of x will first be multiplied by each element of W, giving intermediate values at each hidden node.

These intermediate values are then added to corresponding elements of b; finally, all those intermediary results are fed into y as final outputs.

Gradient Descent for Backpropagation

In its most general form, a feedforward neural network is composed of multiple layers.

Each neuron receives input from one or more neurons from a previous layer, computes an output value, and passes that value on to another set of neurons at a subsequent layer.

Here’s an example of a simple multi-layer neural network with only two layers

Input -> hidden -> output

Mathematically, if we denote each layer by L_i, then our overall model has (L_1 * L_2) inputs going into L_2 outputs.

This equation can be used to derive gradient descent: With gradient descent, we want to find values for w (weights), c (biases), and b (thresholds) that minimize error E between actual y_true values and predicted y values.

Given these w, c, b values, how can we update them so as to minimize E ? We use chain rule: It turns out that backpropagation actually solves an optimization problem of minimizing E via gradient descent!

Backpropagation in Artificial Neural Networks

Here, we will see how backpropagation is applied to Artificial Neural Networks (ANNs). ANNs are a set of interconnected units called neurons.

Each neuron receives input signals from other neurons and based on these signals produces an output signal, which is propagated through other connected neurons.

A neuron with no input signals is referred to as an input neuron, while those without output connections are termed output neurons.

The entire collection of all input and output neurons forms a layer, Typically, layers alternate between input and output layers.

There can be any number of hidden layers, Note that there can be multiple copies of a particular layer within one network: Example three successive hidden layers -hidden1, hidden2, and hidden3 in addition to two input and two output layers.

Related Article: What is an Artificial Neural Network (ANN)?

Conclusion

While most of us are familiar with backpropagation as it applies to artificial neural networks, many people aren’t familiar with how backpropagation can be used for functions and other types of neural networks.

If you’re interested in exploring generalizations of backpropagation, feel free to check out previous articles on continuous-time recurrent neural networks and multilayer perceptions.